Static vs Dynamic Pressure: What’s the Difference?

Static vs Dynamic Pressure: What’s the Difference? A Comprehensive Guide for Instrumentation Professionals

In the world of instrumentation and control, precision is paramount. Whether you’re ensuring the safe flight of an aircraft, optimizing the efficiency of an HVAC system, or controlling a complex industrial process, accurate measurement is the bedrock of your work. Among the most fundamental, yet often misunderstood, parameters are static and dynamic pressure. What do these seemingly interchangeable terms truly mean? And why is a clear grasp of their differences not just academic, but essential for any instrumentation professional or student?

The answer lies in the very heart of fluid dynamics. The graceful lift of an airplane wing, the flow of natural gas through a pipeline, and the ventilation of a cleanroom all hinge on the intricate dance between these two forms of pressure. They are two sides of the same coin, representing the total energy of a fluid in motion.

This in-depth guide is designed for you, the instrumentation professional and the aspiring student. We will demystify these core concepts, moving from foundational definitions to the governing principles that connect them. We’ll explore how they are measured in the real world, complete with diagrams, and examine their critical role in a vast array of applications. By the end of this article, you will not only understand the “what” but also the “why” and “how” of static and dynamic pressure, empowering you to make more accurate measurements and troubleshoot with greater confidence.

Part 1: Defining Static Pressure: The Pressure at Rest

At its core, static pressure is the pressure exerted by a fluid when it is not moving, or the pressure that is independent of the fluid’s bulk motion. Imagine the air inside an inflated car tire. The air molecules are in constant, random motion, colliding with each other and the inner walls of the tire. This ceaseless bombardment exerts a force on the tire’s interior surface, and that force, distributed over the area of the surface, is the static pressure. It is the pressure you would feel if you were moving along with the fluid, a part of the flow itself.

A Molecular Perspective

On a molecular level, static pressure is a manifestation of the internal energy of a fluid. The temperature of a fluid is a measure of the average kinetic energy of its randomly moving molecules. These molecules, in their chaotic dance, exert pressure in every direction. Even in a fluid that is flowing in a specific direction, this random molecular motion persists, giving rise to static pressure.

Key Characteristics of Static Pressure:

Omnidirectional: In a fluid at rest, static pressure acts equally in all directions. This is a restatement of Pascal’s Law. For a moving fluid, this holds true as well; the pressure acts perpendicular to any surface it contacts, regardless of the orientation of that surface within the fluid.
Independent of Fluid Velocity: By definition, static pressure is the pressure component that is not associated with the directional movement (kinetic energy) of the fluid.
Measurement Perpendicular to Flow: To accurately measure static pressure in a moving fluid, the measurement must be taken in a way that does not capture the energy of the flow itself. This is achieved by using a pressure tapping that is flush with the wall of the pipe or duct, oriented perpendicular to the direction of fluid movement.

Analogies for Clarity:

A Still Pool of Water: The pressure you feel on your ears as you dive deeper into a calm swimming pool is static pressure. It increases with depth due to the weight of the water above you, but at any given depth, it is the same in all directions.
An Unopened Soda Can: The pressure inside a can of carbonated beverage before it’s opened is static pressure. The dissolved carbon dioxide exerts a uniform pressure on the can’s inner surfaces.

Block Diagram: Measuring Static Pressure

To measure static pressure in a pipeline, a simple and effective method is the wall pressure tapping. A small, smooth hole is drilled into the wall of the pipe, perpendicular to the flow. This tapping is then connected to a pressure measurement device like a manometer or a pressure transducer. Because the opening is parallel to the flow lines, it does not “feel” the force of the moving fluid, only the random pressure exerted by the molecules.

A block diagram illustrating the measurement of static pressure ( $P_s$ ) using a wall tapping perpendicular to the direction of fluid flow.

In mathematical terms, static pressure is typically denoted as $P_s$ . It’s a fundamental parameter that tells you about the internal state of the fluid.

Part 2: Unveiling Dynamic Pressure: The Pressure of Motion

If static pressure is the pressure a fluid “has,” then dynamic pressure is the pressure it “does” due to its motion. It is the kinetic energy per unit volume of a fluid. It is not a pressure that can be measured directly with a single instrument in the same way as static pressure; instead, it is a calculated value derived from the fluid’s velocity and density.

Think of holding your hand out of a moving car window. The force you feel pushing against your palm is a result of the air’s dynamic pressure. The faster the car moves, the stronger the force becomes. This is because the mass of air hitting your hand per second increases, and you are bringing that air to a relative stop.

Conceptual Foundation

Dynamic pressure represents the increase in pressure that would occur if the moving fluid were to be brought to a complete standstill without any energy loss. It is the pressure equivalent of the fluid’s kinetic energy. Unlike static pressure, which is omnidirectional, dynamic pressure has a specific direction – it acts in the direction of the fluid’s flow.

Key Characteristics of Dynamic Pressure:

Dependent on Velocity and Density: Dynamic pressure is directly proportional to the density of the fluid and, most importantly, to the square of its velocity.
Directional: It is a vector-like quantity that acts in the direction of the fluid’s bulk movement.
Cannot Be Measured Directly: You cannot place a simple pressure gauge in a fluid flow and measure dynamic pressure. It must be calculated or derived from the difference between total pressure and static pressure.

The Power of the Squared Velocity

The relationship between dynamic pressure and the square of the velocity is a critical concept for every instrumentation professional. It means that if you double the velocity of a fluid, you quadruple its dynamic pressure. This non-linear relationship has significant implications for system design, energy consumption in pumping and fan systems, and the forces exerted on objects in a flow.

Mathematical Representation

The formula for dynamic pressure is elegantly simple yet powerful:

$q =1/2 ρ v²$

Where:

$q$ is the dynamic pressure.
$r h o$ (rho) is the density of the fluid.
$v$ is the velocity of the fluid.

This equation is a cornerstone of fluid dynamics and is essential for calculating flow rates and understanding the forces at play in a moving fluid.

Part 3: The Governing Principle: Bernoulli’s Equation and Total Pressure

Static and dynamic pressure are not isolated concepts; they are intrinsically linked by one of the most famous principles in physics: Bernoulli’s principle. Formulated by Swiss mathematician and physicist Daniel Bernoulli in the 18th century, this principle is essentially a statement of the conservation of energy for a flowing fluid.

In its simplified form, Bernoulli’s equation states that for a fluid flowing along a horizontal path, the sum of its static pressure and its dynamic pressure is constant. This constant value is known as the total pressure or stagnation pressure.

Bernoulli’s Equation: The Unifying Link

The relationship is expressed as:

$P_{t} = P_{s} +1/2 ρ v²$

Where:

$P_t$ is the total pressure (stagnation pressure).
$P_s$ is the static pressure.
$f r a c 12$
$r h o v²$ is the dynamic pressure ( $q$ ).

Understanding Total Pressure (Stagnation Pressure)

Total pressure is the pressure measured at a point where the fluid is brought to a complete stop (its velocity becomes zero) in a frictionless manner. At this “stagnation point,” all of the fluid’s kinetic energy (dynamic pressure) is converted into pressure energy. A classic example is the pressure at the very tip of an aircraft’s nose or the leading edge of a wing as it flies through the air. The air at this exact point comes to a momentary halt relative to the aircraft, and the pressure measured there is the total pressure.

The Inverse Relationship: The Venturi Effect

Bernoulli’s equation reveals a crucial inverse relationship between static pressure and fluid velocity (and therefore dynamic pressure). If the total pressure in a system remains constant, and the velocity of the fluid increases, its dynamic pressure must increase. To maintain the balance, the static pressure must decrease.

This phenomenon is vividly demonstrated by the Venturi effect. When a fluid flows through a constricted section of a pipe (a Venturi), it must speed up to maintain the same volume flow rate. According to Bernoulli’s principle, this increase in velocity (and dynamic pressure) in the constricted throat is accompanied by a corresponding drop in static pressure.

Block Diagram: The Venturi Effect

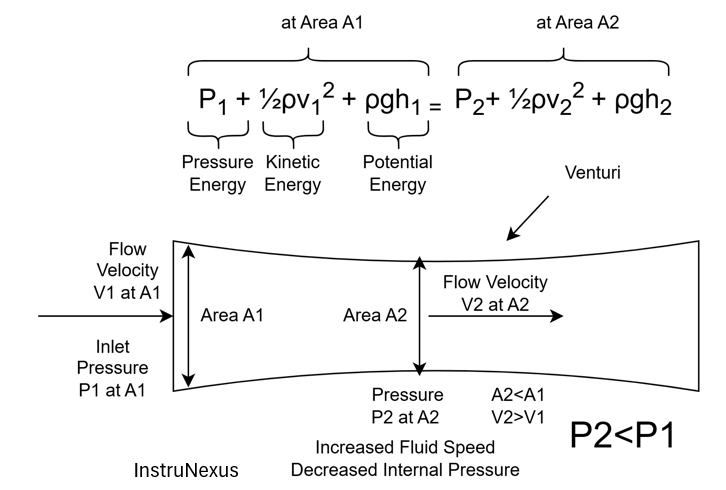
A diagram of a Venturi meter, illustrating how the static pressure decreases as the fluid velocity increases in the constricted throat, a direct consequence of Bernoulli’s principle.

This principle is the foundation for numerous flow measurement devices, as the pressure differential between the wider and constricted sections can be directly correlated to the fluid’s flow rate.

Part 4: Measurement Techniques: From Theory to Practice

Understanding the theory is one thing; measuring these pressures accurately in an industrial setting is another. For instrumentation professionals, mastering the practical techniques is crucial.

Measuring Static Pressure

As previously mentioned, static pressure is measured using a tapping that is perpendicular to the flow. Common instruments connected to these tappings include:

Manometers: Simple, yet effective for visual indication and calibration, using a column of liquid to measure pressure differences.
Pressure Transducers/Transmitters: These devices convert the measured pressure into an electrical signal (e.g., 4-20 mA) that can be sent to a control system or display.

Measuring Total Pressure and Deriving Dynamic Pressure: The Pitot-Static Tube

The most common and ingenious instrument for measuring both static and total pressure simultaneously is the Pitot-static tube (also known as a Prandtl tube). This device is a staple in aerodynamics and industrial flow measurement.

A Pitot-static tube consists of two concentric tubes. The inner tube has an opening at its tip that faces directly into the fluid flow. The outer tube has a series of small holes drilled into its side, parallel to the flow.

Block Diagram: The Pitot-Static Tube

                                      Fluid Flow -> -> -> -> -> -> ->
                               _______________________________________
                              |                                       |
    Total Pressure Port --->  |  Inner Tube                           | ---> To High Pressure Side of DP Sensor
    (Faces Flow)              |_______________________________________|
                              |   |    |    |    |    |    |    |   |  |
                              |  Outer Tube                           |
    Static Pressure Ports --> |___|____|____|____|____|____|____|___|__| ---> To Low Pressure Side of DP Sensor
    (Parallel to Flow)

A detailed block diagram of a Pitot-static tube showing the total pressure port at the tip and the static pressure ports on the side. The difference between these two pressures gives the dynamic pressure.

How it Works: A Step-by-Step Guide

Measuring Total Pressure ( $P_t$ ): The fluid flowing directly into the opening at the tip of the inner tube is brought to a standstill (stagnates). This port, therefore, measures the total pressure – the sum of the static pressure and the dynamic pressure.
Measuring Static Pressure ( $P_s$ ): The holes on the side of the outer tube are parallel to the fluid flow. As the fluid streams past these holes, they are unaffected by the fluid’s kinetic energy. These ports measure only the static pressure of the surrounding fluid.
Determining Dynamic Pressure ( $q$ ): The two pressure outlets from the Pitot-static tube are connected to a differential pressure (DP) sensor or a manometer. This instrument measures the difference between the total pressure and the static pressure:
Differential Pressure = Total Pressure – Static Pressure Differential Pressure = $P_t - P_s$
From Bernoulli’s equation, we know that $P_t - P_s = f r a c 12 r h o v^{2}$ . Therefore, the measured pressure difference is the dynamic pressure!
Calculating Fluid Velocity ( $v$ ): Once the dynamic pressure ( $q = P_t - P_s$ ) is known, and the fluid density ( $r h o$ ) is known, the velocity of the fluid can be easily calculated by rearranging the dynamic pressure formula:
$v =\sqrt 2 q/$ ρ = =√2(Pt−Ps)/ρ

This elegant method allows for the direct calculation of fluid velocity, making the Pitot-static tube an invaluable tool in countless applications.

Part 5: Real-World Applications in Instrumentation

The principles of static and dynamic pressure are not confined to textbooks. They are actively applied every day in a multitude of fields.

Aerospace: The airspeed indicator in every aircraft is essentially a sophisticated differential pressure gauge connected to a Pitot-static tube. By measuring the dynamic pressure, the pilot knows the aircraft’s speed relative to the surrounding air, a critical parameter for safe flight.
HVAC (Heating, Ventilation, and Air Conditioning): In large buildings, Pitot tubes are used to traverse air ducts and measure air velocity. This data is essential for balancing the system, ensuring proper airflow to all areas, and calculating the system’s overall efficiency. Static pressure measurements are used to determine the resistance of filters and ductwork.
Industrial Flow Measurement: Venturi meters, orifice plates, and flow nozzles all operate on Bernoulli’s principle. They create a deliberate change in cross-sectional area to cause a measurable static pressure drop, which is then used to calculate the flow rate of liquids and gases in pipelines for process control.
Automotive Engineering: During the design phase, vehicles are tested in wind tunnels. Arrays of pressure sensors and Pitot tubes are used to map the static and dynamic pressure distribution over the car’s body, helping engineers to optimize its aerodynamic profile, reduce drag, and improve fuel efficiency.
Meteorology: The cup anemometer, a common weather station instrument, works by the principle of dynamic pressure. The wind exerts a greater force on the concave side of the cups than on the convex side, causing them to rotate at a speed proportional to the wind velocity.

Conclusion: A Tale of Two Pressures

In the intricate world of fluid dynamics, static and dynamic pressure are the two fundamental pillars upon which our understanding is built. Static pressure is the uniform pressure a fluid exerts at rest, an intrinsic property acting in all directions. Dynamic pressure is the directed pressure of motion, the kinetic energy of the flow made manifest.

Their relationship, elegantly described by Bernoulli’s principle and captured by the concept of total pressure, is the key that unlocks the ability to measure and control the behavior of fluids. For the instrumentation professional, a deep understanding of this distinction is not just beneficial—it’s indispensable. It empowers you to select the right instruments, install them correctly, interpret data accurately, and ultimately, design and maintain systems that are safe, efficient, and reliable. Mastering these concepts is a significant step towards becoming a true expert in the field of instrumentation.

Frequently Asked Questions (FAQ)

1. Can dynamic pressure be negative?

No, dynamic pressure itself cannot be negative. The formula for dynamic pressure is $q = f r a c 12$

$r h o v²$ . Since fluid density ( $r h o$ ) and the square of velocity ( $v^{2}$ ) are always non-negative, dynamic pressure will always be positive or zero (when the fluid is at rest).

2. Is gauge pressure a static or total pressure? Gauge pressure is a type of pressure measurement, not a type of pressure itself. Gauge pressure is measured relative to the local atmospheric pressure. You can measure both static pressure and total pressure in terms of gauge pressure. For example, a static pressure tapping in a duct might read 0.5 “w.c. (inches of water column) gauge pressure, meaning it is 0.5 “w.c. above the surrounding atmospheric pressure.

3. How does temperature affect static and dynamic pressure measurements? Temperature primarily affects the density ( $r h o$ ) of the fluid. For gases, an increase in temperature at constant pressure leads to a decrease in density. When calculating velocity from dynamic pressure ( $v = s q r t 2 q / r h o$ ), it is crucial to use the correct density for the fluid’s operating temperature. Failure to account for temperature changes can lead to significant errors in velocity and flow rate calculations.

4. What is the difference between a Pitot tube and a Pitot-static tube? A simple Pitot tube has only one opening that faces the flow, and it measures only the total (stagnation) pressure. To find the dynamic pressure and velocity with a simple Pitot tube, you would need a separate static pressure tapping elsewhere in the system. A Pitot-static tube is a more advanced instrument that conveniently combines both a total pressure port and static pressure ports into a single probe, allowing for a direct measurement of the dynamic pressure.

5. Why is it so important to measure static pressure perpendicular to the flow? If the static pressure tapping is not perfectly perpendicular to the flow, it can be influenced by the fluid’s velocity. If the opening is angled even slightly into the flow, it will sense a portion of the dynamic pressure, resulting in a reading that is higher than the true static pressure. Conversely, if it is angled away from the flow, it can create a localized low-pressure area, leading to an erroneously low reading. Accuracy demands a perpendicular orientation.

Static vs Dynamic Pressure: What’s the Difference?