Have you ever marveled at the effortless glide of an airplane, the deceptive curve of a spinning baseball, or even the simple act of a perfume atomizer producing a fine mist? These seemingly disparate phenomena are all governed by a fundamental concept in physics known as Bernoulli’s Principle. It’s a principle that, at its core, describes the elegant relationship between the speed of a fluid (be it a liquid or a gas) and its pressure.
While the name might evoke images of complex equations and daunting textbooks, the essence of Bernoulli’s Principle is surprisingly intuitive and can be observed in countless everyday situations. This blog post aims to demystify this cornerstone of fluid dynamics, offering a comprehensive yet simple explanation of how it works, where we see it in action, and how to avoid common misunderstandings. So, buckle up as we embark on a journey into the fascinating world of the physics of flow.
The Core Idea: When Speed Increases, Pressure Decreases
At its heart, Bernoulli’s Principle, formulated by the Swiss mathematician and physicist Daniel Bernoulli in the 18th century, states that for a fluid in motion, an increase in speed occurs simultaneously with a decrease in pressure or a decrease in the fluid’s potential energy. To put it even more simply: where a fluid moves faster, it exerts less pressure.
This inverse relationship between velocity and pressure is a direct consequence of the conservation of energy. Imagine a small parcel of fluid moving along a streamline (the path a particle of fluid follows). For this parcel to accelerate and increase its speed, a net force must act upon it. This force arises from a difference in pressure. For the parcel to speed up, the pressure behind it must be greater than the pressure in front of it. Therefore, the region of higher velocity is also a region of lower pressure.
Unpacking Bernoulli’s Equation: The Conservation of Energy in Fluids
For those who appreciate the mathematical elegance behind physical principles, Bernoulli’s equation provides a quantitative expression of this relationship. In its common form, for a fluid flowing horizontally, it is written as:
Where:
- P is the pressure of the fluid.
- ρ (rho) is the density of the fluid.
- v is the velocity of the fluid.
This equation essentially states that the sum of the static pressure (P) and the dynamic pressure () at any two points in a horizontal flow are equal. If the velocity (v) increases, the pressure (P) must decrease to maintain this equality, and vice versa.
A more general form of Bernoulli’s equation also accounts for changes in potential energy due to changes in height:
Here:
- g is the acceleration due to gravity.
- h is the height of the fluid above a reference point.
This complete form beautifully illustrates the principle of conservation of energy applied to a moving fluid. It tells us that the total energy of a fluid element—comprising its pressure energy (P), kinetic energy per unit volume (), and potential energy per unit volume (ρgh)—remains constant along a streamline.
Think of it like a roller coaster. At the top of a hill (high potential energy), its speed (kinetic energy) is low. As it descends, its potential energy is converted into kinetic energy, and its speed increases. Similarly, in a fluid, energy can be converted between pressure, kinetic, and potential forms.
Visualizing the Flow: Block Diagrams Explained
To make this concept even clearer, let’s use some simple block diagrams.
Diagram 1: The Basic Principle – A Venturi Tube
Imagine a pipe that narrows in the middle and then widens again. This is known as a Venturi tube.
Explanation of the Venturi Tube Diagram:
- Region 1 (Wide Section): The fluid enters with a certain velocity (v1) and pressure (P1).
- Region 2 (Narrow Section): To pass through the constricted section, the fluid must speed up. According to the principle of continuity (what goes in must come out), the velocity (v2) in the narrow section will be higher than v1. As a result of this increased speed, Bernoulli’s principle tells us that the pressure (P2) in this section will be lower than P1.
- Region 3 (Wide Section): As the pipe widens again, the fluid slows down to a velocity (v3) similar to v1. Consequently, the pressure (P3) increases again, approaching the initial pressure P1 (ignoring any frictional losses).
This Venturi effect is not just a theoretical curiosity; it’s the operational principle behind many devices, including carburetors in older cars and some types of flow meters.
Diagram 2: Energy Transformation in a Fluid
This block diagram illustrates the conservation of energy aspect of Bernoulli’s principle.
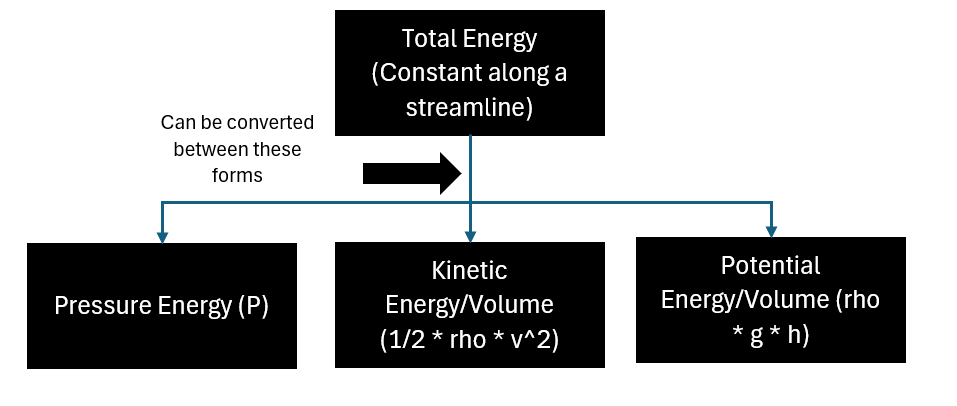
Explanation of the Energy Transformation Diagram:
This diagram emphasizes that the total energy of a fluid element is a fixed sum. If one component, say kinetic energy (due to an increase in velocity), goes up, one or both of the other components (pressure energy or potential energy) must decrease to maintain the balance.
Everyday Encounters with Bernoulli’s Principle
Once you understand the core concept, you’ll start seeing Bernoulli’s principle at play all around you. Here are some of the most common and compelling examples:
1. The Magic of Flight: How Airplanes Generate Lift
This is perhaps the most famous application of Bernoulli’s principle. The cross-section of an airplane wing, known as an airfoil, is designed with a curved upper surface and a flatter lower surface.
- Faster Air Above: As the plane moves forward, the air splitting at the leading edge of the wing has to travel a longer distance over the curved top surface compared to the flatter bottom surface to meet at the trailing edge at roughly the same time. This means the air flowing over the top of the wing must move faster than the air flowing underneath.
- Pressure Difference: According to Bernoulli’s principle, this higher-speed air above the wing creates a region of lower pressure compared to the slower-moving, higher-pressure air below the wing.
- Upward Force: This pressure difference results in a net upward force on the wing, which we call lift. When this lift force is greater than the weight of the airplane, it takes to the skies.
Block Diagram: Airplane Wing and Lift
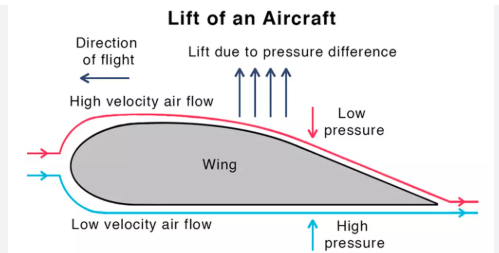
2. The Curveball’s Deception
A spinning baseball is another classic example. When a pitcher throws a curveball, they impart a significant spin on the ball.
- Spin and Airflow: As the spinning ball moves through the air, one side of the ball is moving in the same direction as the airflow, while the other side is moving against it.
- Velocity Difference: The side of the ball spinning with the airflow experiences a higher relative velocity of air, while the side spinning against the airflow experiences a lower relative velocity.
- Pressure Imbalance: This velocity difference creates a pressure differential. The side with the faster-moving air has lower pressure, and the side with the slower-moving air has higher pressure.
- Deflected Path: The ball is then pushed from the high-pressure side to the low-pressure side, causing it to curve in its path, much to the batter’s dismay.
3. The Simple Perfume Atomizer
A perfume atomizer or a paint sprayer is a textbook demonstration of Bernoulli’s principle.
- High-Speed Airstream: When you squeeze the bulb, you force a jet of air to move at high speed across the top of a small tube that dips down into the perfume.
- Low Pressure Creation: This fast-moving air creates a region of low pressure above the tube.
- Liquid Drawn Up: The atmospheric pressure inside the bottle, which is now higher than the pressure above the tube, pushes the perfume up the tube and into the airstream.
- Fine Mist: The high-speed air then breaks the liquid into a fine mist.
4. The Shower Curtain Phenomenon
Have you ever noticed how the shower curtain seems to billow inwards when you turn on the water? That’s Bernoulli at work in your bathroom.
- Moving Air and Water: The stream of water from the showerhead entrains the surrounding air, creating a flow of air and water inside the shower.
- Lower Pressure Inside: This moving fluid (air and water droplets) inside the shower has a higher velocity than the still air outside the curtain.
- Pushed Inwards: This results in lower pressure inside the shower compared to the higher atmospheric pressure outside. The higher pressure outside then pushes the shower curtain inwards.
Debunking Common Misconceptions
While Bernoulli’s principle is a powerful explanatory tool, it is also one of the most frequently misapplied principles in introductory physics. It’s crucial to understand its limitations and the common fallacies associated with it.
-
The “Equal Transit Time” Fallacy: One of the most persistent myths, often used to explain airplane lift, is the idea that the air particles that split at the leading edge of the wing must meet up at the trailing edge at the same time. This is simply not true. In reality, the air traveling over the top of the wing moves significantly faster and arrives at the trailing edge sooner. The lift is a consequence of the velocity difference, not a result of “equal transit time.” The actual explanation of lift is a complex interplay of Bernoulli’s principle and Newton’s third law of motion (for every action, there is an equal and opposite reaction – the wing pushes air down, and the air pushes the wing up).
-
Blowing the Roof Off: A common example given for Bernoulli’s principle is a hurricane blowing the roof off a house. The explanation often goes that the high-speed wind over the roof creates low pressure, and the higher pressure inside the house pushes the roof off. While there is a grain of truth to this, it’s an oversimplification. The reality is far more complex, involving significant pressure fluctuations, turbulence, and the geometry of the building. While Bernoulli’s principle plays a role, it’s not the sole or even the primary cause in many cases.
-
Applicability to Confined vs. Unconfined Flow: Bernoulli’s principle is most accurately applied to fluids flowing within a confined space, like a pipe or a Venturi tube. In unconfined flows, such as the air moving over a car, the interactions are more complex, and other factors like turbulence and viscosity play a significant role.
The Broader Significance: From Engineering to Medicine
The applications of Bernoulli’s principle extend far beyond the examples mentioned above. It is a fundamental concept that underpins many technologies and natural phenomena:
- Carburetors and Fuel Injectors: In older engines, the Venturi effect in a carburetor was used to draw fuel into the engine’s intake air. Modern fuel injectors use similar principles to atomize fuel.
- Bunsen Burners: The gas jet from the nozzle of a Bunsen burner moves at high speed, creating a low-pressure area that draws in air from the surrounding environment for combustion.
- Medical Applications: Bernoulli’s principle is used to understand blood flow in arteries. A narrowing of an artery (stenosis) will cause the blood to flow faster at that point, leading to a decrease in pressure. This can have significant physiological consequences. It also plays a role in the measurement of blood pressure.
- Industrial Processes: Many industrial processes that involve the transport of fluids, from chemical manufacturing to water treatment, rely on the principles of fluid dynamics, including Bernoulli’s equation.
Conclusion: An Elegant Principle Governing the Unseen
Bernoulli’s principle is a testament to the underlying simplicity and elegance of the laws of physics. It reveals a fundamental truth about the behavior of fluids: speed and pressure are inextricably linked. From the majestic flight of an eagle to the simple act of blowing over a piece of paper and watching it rise, this principle is constantly at work, shaping the world around us in ways both profound and subtle.
By understanding this principle, we gain a deeper appreciation for the intricate dance of forces that govern the flow of liquids and gases. It reminds us that even the most complex phenomena can often be understood through a grasp of fundamental concepts. So, the next time you see a plane soaring overhead or a leaf fluttering in the wind, take a moment to appreciate the invisible forces at play, all orchestrated by the timeless and elegant physics of flow, as described by Daniel Bernoulli over two and a half centuries ago.

